Worksheet 4: Physician agency

Denote the quantity of care consumed by $x$ , and denote by $B (x)$ the function that determinesthe benefit of care to the patient. Assume that the patient must pay the full price of care, $p x$ , so that their net benefit is $N B = B (x) - p x$ .

Question 1:

Find the patient’s optimal $x$ .

The patient just wants to maximize their net benefit, $B (x) - p x$ . Taking the derivative and setting to 0, this means $B^{'} (x) = p$ (i.e., marginal benefit to the patient is equal to the patient’s marginal cost).

Question 2:

Draw the marginal benefit on a graph and note the price and patient’s optimal quantity.

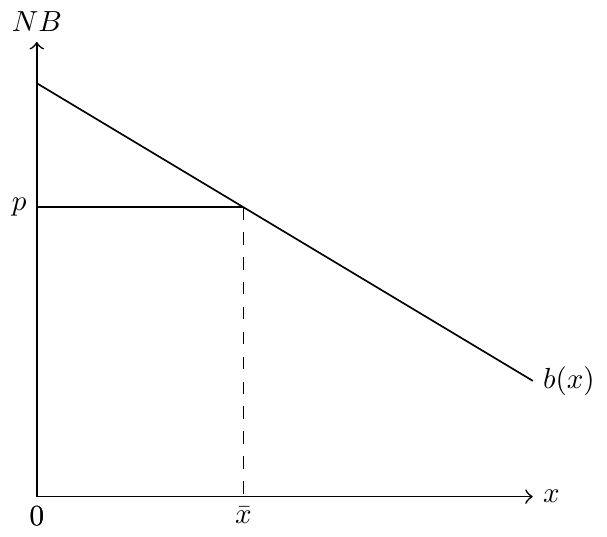
Question 3:

Find the physician’s optimal $x$ assuming $N B^{0} = 0$ .

The physician is profit maximizing, subject to the constraint that $N B^{0} = B (x) - p x = 0$ . Plugging this constraint into the profit function yields, $π = B (x) - N B^{0} - c x = B (x) - c x$ . Taking the derivative and setting it to 0 yields the expression, $B^{'} (x) = c$ . So the physician also set’s marginal benefit equal to marginal cost…they just focus on their own marginal cost instead of the marginal cost to the patient.

Question 4:

Add the physician’s optimal $x$ to your graph and interpret the difference.